有限元建模

前处理的重要性

        有限元方法已经迅速从结构工程强度分析计算扩展到几乎所有的科学技术领域。随着数值分析方法的逐步完善和计算机运算速度的飞速发展,整个计算系统用于求解运算的时间越来越少,而数据准备（前处理）和运算结果的表现问题却日益突出。前处理工作成为CAE工作的重中之重。为建立正确、合理的有限元模型，需要把握好模型的简化、布局合理的网格密度以及确保网格的质量等。

       高质量的网格是高精度分析结果的保证，而质量不好或者差的网格，则可能会导致计算的无法完成或者得到无意义的结果。在一个完整的分析计算过程中，与网格设计与修改相关的前处理工作占到了CAE工程师工作量的60%-70%，CAE工程师往往要花费大量的时间来进行网格处理，所以主要的瓶颈在于如何快速准备好高质量的满足分析计算要求的网格。

       准备高质量的分析模型是一件很费时间和精力的事情，而且要求前处理工程师能够根据CAE工程师提出的分析要求设计出能满足CAE工程师分析要求的合适的网格，然后提交给CAE工程师进行分析计算。所以前处理工程师应当具有相当的技术经验和背景，才能完成高质量的网格。

前处理的考虑因素

        理论上讲，模型中使用的单元越多，结果就越接近真实结果。然而，我们不可能去分析无限多的单元，一方面是为了节省计算资源；另一方面需要找到计算的规模（网格数量）和计算的准确性之间的平衡。因此，前处理工程师需要从以下几个方面进行综合考虑：

        要进行什么类型的分析计算？非线性分析往往比线性分析有更严格的网格要求。例如滑动接触问题可能需要一个更精细的网格来捕捉变化的状态行为；高级材料，如塑性、超弹性等，通常需要更精细的网格来捕捉大应变梯度；大变形分析需要更精细的网格来适应分析过程中形状的大变化

        关注的区域在哪里？如果事先知道关注区域在哪里，与其细化整体网格，不如将单元集中在关注的区域，粗网格通常足够用于力传递，可以用于不需要应力信息的区域。如果事先不知道关注的区域，可先进行粗网格分析，确定后续分析中需要细化的区域。

        小特征将会如何影响结果？小孔、圆角、凸角、窄边都将自动生成一个非常精细、局部化的网格。我们需要评估这些特性是否会影响分析：它是否在关键区域？它会影响加载路径吗？这些需要用户在求解精度和时间中做出权衡。

        需要一个什么样的结果？定性还是定量？对于线性分析，精确的位移结果不需要像应力结果那样精细的网格——如果分析是为了确保位移不会太大，那么可以使用较粗的网格，如果分析需要评估结构的应力，在关键的区域需要加密网格。

         使用什么样的单元？有些单元在弯曲时比较“刚”，需要在零件的厚度上加密网格来正确地捕捉弯曲行为。这类问题通常被称为“锁定”，原则上有中间节点的单元（二次单元）比线性单元更不容易被锁定，但如果弯曲非常显著，即使使用带中节点的单元，也建议厚度上大于一个单元。此外，某些单元的形状对变形更敏感。例如，一个六面体单元可以拉长，但仍然提供良好的结果。然而，一个四面体单元在一个方向上伸长时会产生小角度，这可能会提供不那么精确的结果。

        1. 复杂结构的中面网格，主要针对薄壁件尤其是汽车，航天航空，电子这个行业里大量存在，像手机、汽车上的仪表板、汽车的车身，这样的结构件单元很薄，很难用实体单元来描述。用壳单元描述更合适一些。用壳单元描述，就首先要得到这个结构的几何中面。一般来说像塑料件、薄壁件有一个共同的特点就是结构比较复杂，有很多的筋、圆孔等等。难度在于如何得到这个复杂结构的中面网格，几何上有圆角、加强筋、圆孔等等，抽完中面之后，怎样把它们连接起来；得到几何之后如何保证高质量的面网格。

        2. 复杂结构的六面体，像结构体，譬如发动机的缸盖、活塞、缸体、曲轴、转向节、变速箱的壳体，这样的结构最好的形式是用六面体，因为六面体精度比较高。六面体的生成完全依靠人工来完成，这就需要非常专业的工程师才能完成。

        3. 比较复杂的网格，就是流体网格CFD网格。流体网格几何的外表面是封闭的，对于一个结构来说，比如整车，导弹的外流场，飞机等的外流场，有大量的曲面间隙需要去缝合修补，要生成面网格，还要考虑附面层，流体网格的特点是几何清理极其复杂，工作量特别大，对附面层的质量要求非常苛刻。根据你选择的不同的流体方程，附面层网格的质量有不同的要求。

网格质量

        单元的质量是非常主观的——一套网格在一组边界条件和载荷下给出好的结果，在另一组边界条件和载荷下可能给出糟糕的结果。然而，它依然不失为一个有用的工具来大致了解网格的质量好坏。下面列出了一些常见的质量度量标准：

        Aspect ratio。Aspect ratio是单元的最长边与最短边的比值。理想的单元具有1的长宽比，但是正如前面提到的，一些单元（如六面体）对大的高宽比不太敏感。

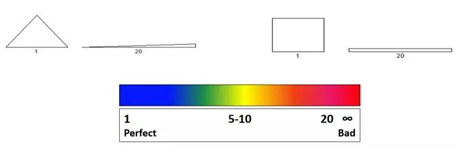
       Skewness。Skewness衡量一个单元的面有多接近理想情况。值的范围从0（理想）到1（退化）。它是通过比较实际单元的大小和理想单元的大小来计算的，理想单元的大小可以与原始单元在相同大小的圆内匹配。

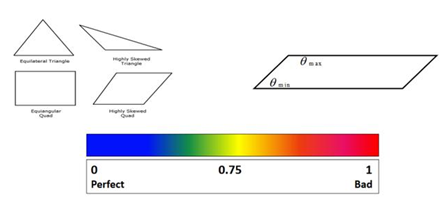
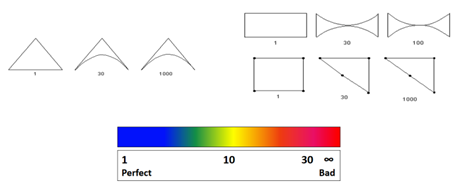
        Jacobian Ratio。该比值基于雅可比矩阵的行列式，在有限元分析中，雅可比矩阵用于将单元矩阵从理论形状（如完全平方、三角形）转换为实际形状。理想单元的雅可比矩阵比为1，该值离1越远，该单元网格质量也越差。

 铁力士科技的经验

       铁力士科技多年来承接了汽车、轨道交通、航空航天、医学生物工程等多个行业的上百个项目，积累了丰富的工程经验以及软件使用经验。可以为客户提供高质量的网格设计服务，可以熟练应用ANSA、HyperMesh、ANSYS和其他常用的网格划分工具来进行网格生成，包括结构网格和流体网格，网格类型涵盖了壳网格、四面体网格、六面体网格以及多面体网格等，在确保网格质量的前提下，实现快速及时的网格划分，从而为您节省大量的时间和精力，使得您可以集中精力于实际工程问题的分析与求解。网格质量好、效率高。如整车（含白车身加闭合件、底盘、动力总成）的网格我们一般只需1个月左右时间完成。